Одним из примеров экстремальной задачи может служить задача максимизации прибыли предприятия в условиях ограниченных ресурсов. Пусть некоторое предприятие, применяя имеющуюся технологию, может выпускать n видов продукции, используя m видов ресурсов. Целью предприятия является получение максимальной прибыли.
Построим математическую модель и целевую функцию для решения задачи определения наиболее прибыльного объема выпуска продукции. То есть такого объема, который может обеспечить предприятию получение максимальной прибыли.
Для
построения математической модели введем следующие обозначения. Обозначим через
![]() ,
, ![]() количество выпускаемой продукции j-го вида. Тогда объем всей
выпускаемой продукции можно обозначить с помощью вектора
количество выпускаемой продукции j-го вида. Тогда объем всей
выпускаемой продукции можно обозначить с помощью вектора ![]() =
=![]() . Обозначим через
. Обозначим через
![]()
![]() запас i-го вида ресурса, имеющийся на предприятии, а через
запас i-го вида ресурса, имеющийся на предприятии, а через
![]() (x),
(x), ![]() - количество i-го ресурса, необходимого для выпуска
продукции, определяемой вектором х.
- количество i-го ресурса, необходимого для выпуска
продукции, определяемой вектором х.
Заметим,
что функции ![]() (x), как правило, определяются используемой на предприятии
технологией.
(x), как правило, определяются используемой на предприятии
технологией.
Очевидно, что выпуск продукции будет ограничен имеющимися запасами ресурсов. Математически эти ограничения можно записать в следующем виде:
![]()
![]() (1)
(1)
Обозначим
через ![]() ,
, ![]() верхние ограничения, обусловленные спросом, на продукцию
j-го вида, а через
верхние ограничения, обусловленные спросом, на продукцию
j-го вида, а через ![]() ,
, ![]() , нижние ограничения обусловлены спросом, на ту же продукцию.
Очевидно, что выпуск продукции должен удовлетворять условиям спроса.
Математически эти условия можно записать следующим образом:
, нижние ограничения обусловлены спросом, на ту же продукцию.
Очевидно, что выпуск продукции должен удовлетворять условиям спроса.
Математически эти условия можно записать следующим образом:
![]()
![]() (2)
(2)
Естественно также, что выпуск
продукции ![]() ,
, ![]() удовлетворяет условиям неотрицательности, а именно
удовлетворяет условиям неотрицательности, а именно
![]()
![]() .
.![]() (3)
(3)
Обозначим через f(x) прибыль, получаемую предприятием от реализации продукции. Тогда задача определения объема выпуска продукции, обеспечивающего предприятию максимальную прибыль, может быть записана следующим образом.
Найти
![]()
![]() (4)
(4)
при условиях (1), (2), (3).
При этом функция f(x) называется целевой функцией, вектор x - вектором переменных, система неравенств (1),(2),(3) представляет собой математическую модель задачи. Иногда систему неравенств вида (1)-(3) называют ограничениями задачи.
Экстремальную задачу (4), (1)-(3) называют также задачей математического программирования или задачей оптимизации.
Дадим
интерпретацию экстремальной задачи (4), (1)-(3) как задачи принятия решения.
Компоненты вектора переменных ![]() ,
, ![]() моделируют принятие конкретного решения. Целевая функция f(x)
моделирует эффективность принимаемого решения. Ограничения (1)-(3) задачи
моделируют связи, накладываемые на компоненты вектора переменных
моделируют принятие конкретного решения. Целевая функция f(x)
моделирует эффективность принимаемого решения. Ограничения (1)-(3) задачи
моделируют связи, накладываемые на компоненты вектора переменных
![]() ,
,![]() способами использования ресурсов.
способами использования ресурсов.
В общем случае экстремальную задачу можно определить, например, следующим образом.
Дано множество X и функция f(x), определенная на множестве X. Требуется найти ( если они существуют ) точки максимума или минимума функции f(x) на множестве X. Условимся записывать задачу максимизации функции f(x) на множестве X следующим образом:
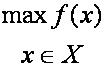 (5)
(5)
При этом функцию f(x) будем по-прежнему называть целевой функцией, вектор x - вектором переменных, множество X будем называть множеством допустимых решений.
Множество X определяется неравенствами (1), (2), (3).
Конкретизируем рассмотренную выше задачу.
Предприятие может выпускать n
видов продукции, используя для этого m видов
ресурсов. Пусть для производства одной единицы продукции
![]() -го вида используется
-го вида используется
![]() единиц ресурса
единиц ресурса ![]() -го вида. Прибыль от реализации одной единицы продукции
-го вида. Прибыль от реализации одной единицы продукции
![]() -го вида обозначим через
-го вида обозначим через
![]() ,
, ![]() рублей. Требуется определить такой объем выпуска продукции,
который обеспечивает предприятию наибольшую прибыль.
рублей. Требуется определить такой объем выпуска продукции,
который обеспечивает предприятию наибольшую прибыль.
Обозначим
через ![]() ,
, ![]() объем продукции j - го вида,
выпускаемой в соответствии с некоторым планом. Тогда математическую модель
задачи можно записать в следующем виде
объем продукции j - го вида,
выпускаемой в соответствии с некоторым планом. Тогда математическую модель
задачи можно записать в следующем виде
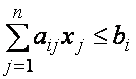
![]() (6)
(6)
Эта модель определяется ограничениями на выпуск продукции, обусловленными имеющимися запасами ресурсов. Целевую функцию задачи можно записать следующим образом
 (7)
(7)
После построения математической модели и записи целевой функции задача определения объема выпуска продукции, обеспечивающего предприятию наибольшую прибыль, может быть сформулирована как задача
Найти max
 (8)
(8)
при условии
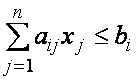
![]() (6)
(6)
![]()
![]() (9)
(9)
Условие (9), указывающее на неотрицательность выпуска продукции, необходимо задавать для решения задачи на компьютере, с использованием EXCEL 2000.
В задаче
(8), (6), (9) отсутствуют ограничения по спросу на продукцию, которым в рыночной
экономике принадлежит важная роль. Введем эти ограничения в задачу следующим
образом. Обозначим через ![]() ,
,![]() верхнее ограничение по спросу на продукцию
верхнее ограничение по спросу на продукцию
![]() -го вида, а через
-го вида, а через
![]() нижнее ограничение по спросу на продукцию
нижнее ограничение по спросу на продукцию
![]() -го вида, тогда задача (8), (6), (9) примет следующий вид
-го вида, тогда задача (8), (6), (9) примет следующий вид
Найти max
 (8)
(8)
при условии
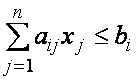
![]() (6)
(6)
![]()
![]() (10)
(10)
![]()
![]() (9)
(9)
В общем случае прибыль с ростом объема производства может начать уменьшаться из-за дополнительных затрат, связанных, например, с реализацией продукции.
Обозначим
через ![]()
![]()
![]()
![]() степень влияния на прибыль объема выпуска
j-го изделия. Тогда целевая функция задачи может быть записана в
следующем виде:
степень влияния на прибыль объема выпуска
j-го изделия. Тогда целевая функция задачи может быть записана в
следующем виде:
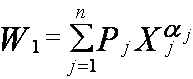 (11)
(11)
а сама задача примет вид
.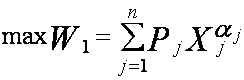 (12)
(12)
при условиях (6), (10), (9).
Заметим, что если
![]() , то прибыль не зависит от объема выпуска j-го
изделия.
, то прибыль не зависит от объема выпуска j-го
изделия.
Имеется m пунктов производства и n пунктов потребления.
Количество
продукта в ![]() -м пункте производства обозначим через
-м пункте производства обозначим через
![]() ,
, ![]() ;
;
Потребность
в продукте в j-м пункте потребления обозначим
через ![]() ,
, ![]()
Стоимость
перевозки одной единицы продукта из ![]() -го пункта производства в j-й пункт
потребления обозначим через
-го пункта производства в j-й пункт
потребления обозначим через ![]() (
(![]()
![]() ) рублей.
) рублей.
Требуется составить такой план перевозки однородного продукта так, чтобы общая стоимость перевозок была минимальной.
Обозначим
через ![]() количество продукта, перевозимого из
количество продукта, перевозимого из
![]() -го пункта в
-го пункта в ![]() -й пункт .
-й пункт .
В принятых обозначениях
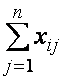 количество продукта, вывозимого из
количество продукта, вывозимого из
![]() -го пункта
-го пункта
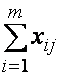 количество продукта, доставляемого в
количество продукта, доставляемого в
![]() -й пункт.
-й пункт.
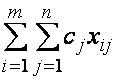 суммарные транспортные расходы.
суммарные транспортные расходы.
Математическая модель транспортной задачи будет иметь следующий вид:
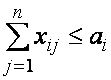
![]() (13)
(13)
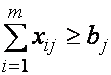
![]() (14)
(14)
![]()
![]()
![]() (15)
(15)
Целевая функция может быть записана следующим образом
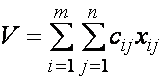 (16)
(16)
Минимизация транспортных расходов требует решения следующей задачи.
Найти min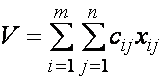 (17)
(17)
при условиях:
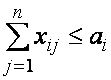
![]() (13)
(13)
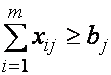
![]() (14)
(14)
![]()
![]()
![]() (15)
(15)
[ на главную ] [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11]